Rim nos pregunta (hemos traducido tu correo del lenguaje SMS al castellano, espero que no te importe, Rim

):
Buenas a aquellos que están al otro lado. Tengo una pregunta que no sé si es inútil pero cuanto menos es curiosa. ¿Cuál es la forma concreta de la curva esta de los skate park? Sí ésta que hace como una "U". Pregunto porque hoy mi profesora de matemáticas ha insinuado que tiene una forma concreta y estudiada, es decir, que no está hecha al azar, y yo que no sabía dónde acudir a prguntar, pues me acordé de vosotros. Ésa es mi pregunta y a ser posible también el porqué. Y de la forma más sencilla que con 16 añitos no doy para mucho, jeje. Bueno, un beso y un saludo y gracias por esas horas que paso descubriendo cosas con vosotros.
PD: Disculpen las faltas ortográficas, pero son las 23:14 y no tengo ganas de ponerme a escribir correctamente, qué malos son los móviles :-p
Pues tu pregunta me parece curiosísima. Pero me temo que no hay demasiado misterio detrás.
Half pipe significa en inglés "media tubería". Supongo que porque los primeros patinadores que empezaron a hacer acrobacias con un patinete utilizaron lo que encontraban por ahí. ¿Y cuál es la forma de media tubería? Pues media circunferencia, claro está. Ahí tienes la forma de tu half pipe. Los bordes elevados tienen forma de un cuarto de circunferencia. Posteriormente se añadió una parte recta en el centro para dar tiempo a preparar la siguiente acrobacia.
Si buscas en Google cómo fabricarte tu propio half pipe, hay algunas páginas que te dan planos más o menos detallados. En
uno de estos planos [.png, 2,12 MB] se aprecia claramente que la forma es de un arco de circunferencia:
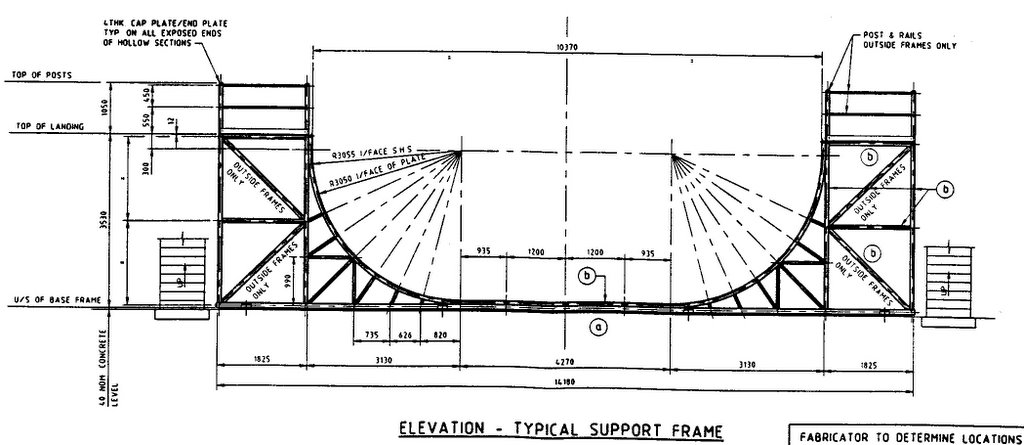
Veámoslo con un poco más de detalle:
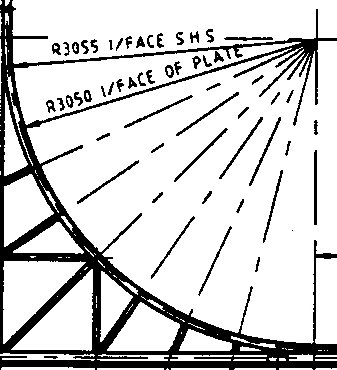
Se puede apreciar claramente que los apoyos de madera son en realidad radios de una cirunferencia. Como los apoyos son perpendiculares a la estructura de la rampa (para evitar momentos y maximizar la resistencia), concluimos que la rampa es circular.
También el snowboard ha heredado esta forma para sus half pipes. Actualmente hay una empresa (
Pipe Dragon) que hace casi todos los half pipes de nieve en acontecimientos importantes. Hicieron los half pipes de los JJ.OO. de Nagano, de Salt Lake City y de Turín. Para hacer un half pipe, primero excavan una ruta rectangular en la ladera y luego le repasan los bordes con el Pipe Dragon:

Se ve que el brazo que usan para dar forma a los bordes de la pista tiene forma de cuarto de circunferencia:

Y además lo dicen en las
especificaciones de su máquina: tienen brazos de 12 y 17 pies de radio. Si sólo dan el radio, es que es una circunferencia.
Pero esta pregunta de Rim me sugiere unas cuantas ideas, todas ellas CPI. ¿Por qué es una forma de medio círculo? Yo lo tengo claro, empezó siendo medio círculo porque era lo que había (restos de grandes tuberías), y ha seguido siéndolo por "tradición" y porque es más fácil de construir. Pero hay otras posibilidades.
Para examinar la primera de ellas, tenemos que remontarnos al año 1696. Ese año Johann Bernoulli publica un "desafío" en
Acta Eruditorum. Se trata de hallar una curva sobre la que una pelota tarde el menor tiempo posible en deslizarse desde un punto A hasta un punto B, actuando sólo la gravedad. Se le llamó el problema de la
Braquistocrona, del griego "el tiempo más corto". Galileo había hecho la hipótesis de que esta curva era un arco de circunferencia, pero estaba equivocado. Cinco matemáticos resolvieron el problema: Newton, Jacob Bernoulli (hermano de Johann), Leibniz y L'Hôpital, además del propio Johann Bernoulli. La solución es que el recorrido sea un trozo de cicloide. ¿Y qué es una cicloide? No pondré la fórmula, pero sí una imagen ilustrativa: la cicloide es la trayectoria que sigue un punto situado en el borde de una rueda cuando ésta gira sin deslizar:



Si le damos la vuelta a la cicloide, quedará una especie de cuenco. Una canica dpositada en este cuenco, fuera del centro, tardará exactamente lo mismo en llegar al punto más bajo, independientemente de a qué altura la dejemos (¡!). Se trata del problema de la tautocrona (igual tiempo), resuelto por Huygens.

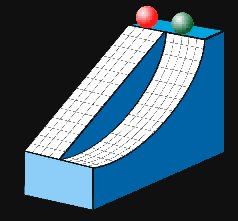
Imagen del museo
Mathematikum, el primer museo de las matemáticas del mundo, en la ciudad de Gießen, Alemania. La rampa azul consta de una línea recta y una braquistocrona. La bola que cae por la braquistocrona cae antes que la de la línea recta, a pesar de que recorre más distancia. En la rampa roja hay dos carriles. Es una tautocrona. Si se colocan dos bolas a diferentes alturas llegan a la parte de abajo al mismo tiempo. La bola que está más arriba recorre mayor distancia pero alcanza mayor velocidad porque la pendiente es mayor.
Actualización: Odo (¡gracias!) nos manda una animación estupenda sobre tres canicas oscilando en una curva tautocrona, con diferentes amplitudes. Se aprecia cómo los periodos son los mismos para las distintas amplitudes:

Volviendo a las cicloides, si el punto no está en el borde de la rueda, sino en el interior, tendríamos una cicloide
contraída reducida (en el cole me dijeron que se llama hipocicloide, pero ahora no estoy muy seguro).
Actualización Pues no se llama hipocicloide, sino cicloide reducida. Véase
este comentario de Dani (¡gracias!):



¿Qué tiene esta nueva curva de especial: Pues que la forma de la caja de resonancia de los violines está hecha con secciones de
hipocicloides cicloides reducidas. Ahí es nada.
Una última curva especial, sobre la que Patxi y Masgon me han hablado más de una vez: la catenaria. Cuando colgamos un cable de dos puntos, éste se curva por su peso: Galileo supueso (de nuevo, incorrectamente), que el cable adoptaba forma parabólica. En realidad, es un coseno hiperbólico. Esta curva tiene la ventaja de que si se la invierte aparece un arco que no tiene ninguna tensión transversal. Gaudí, de nuevo Gaudí, la utilizó profusamente.
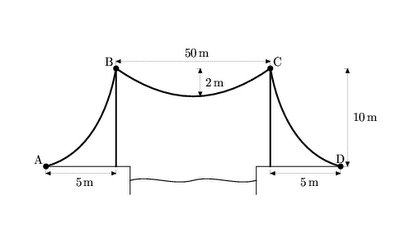 Esquemilla de un puente con cables colgantes en forma de catenaria
Esquemilla de un puente con cables colgantes en forma de catenariaComo dato CPI, en el argot de los trenes se llama la catenaria a todo el conjunto de alimentación eléctrica: los cables (que esos sí tienen forma de catenaria), las torres que sostienen los cables y toda la pesca. Pero a los de la RENFE (Rogamos Empujen Nuestros Ferrocarriles Estropeados) se les puede perdonar cualquier sinécdoque, qué demonios.
Categorías: Consultorio CPI , MatemáticasRecordatorio: ¡Está abierto el concurso de imágenes CPI! ¡Enviadnos imágenes! Y ya tenemos lista la galería de imágenes

















